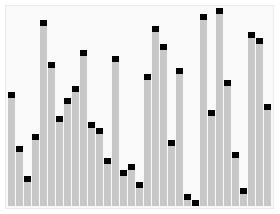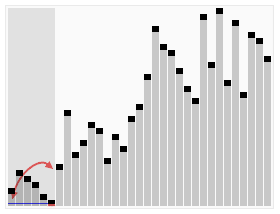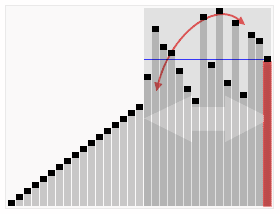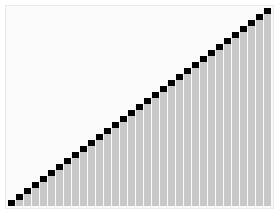
中譯「快速排序法」,該排序演算法是普遍被認為最快的排序演算法,與 merge sort 一樣,都採用 divide & conquer 的策略。不過在切割的部分與 merge sort 不同的是,merge sort 每次切割都是剖半,而 quick sort 則與該次切割時所選的 pivot 有關。
Quick sort 的切割方式為,每次從數列中選出一個元素作為 pivot(支軸),並將剩餘的元素分為兩堆,一堆是小於 pivot 的元素,另一堆是大於 pivot 的元素,至於相等的隨便放就好。也因此造成 quick sort 切割後會有兩堆大小不一樣大的情況。此外,quick sort 切割後,pivot 並不會傳遞下去,因此每次遞回的總元素數量都會減一。所以在切割的停止時機其實可以設定為,已沒有元素可進行切割時。
在合併的部分,在切割的時候其實已經把順序關係給找出來了,切割時我們就可以找到三個部分,分別是:小於 pivot、pivot 與大於 pivot 的三個部分。因此在合併時也按照這樣的順序串接即可!具體的演算法流程,以下分為切割與合併兩個部分:
Divide
- 從數列找出一個元素作為 pivot
- 將小於 pivot 的元素放在一堆,其餘的放在另外一堆
- 持續切割新的子數列直到子數列為空時回傳
Conquer
- 按照順序串接小於 pivot 的部分、pivot 與大於等於 pivot 的部分
時間與空間複雜度
一樣從切割的部份開始,由於要將所有元素都與 pivot 比較一遍,因此需要遍歷數列中的所有元素,時間複雜度為 O(n)。而合併的部分可能依照實作的方式不同而有所差異,但頂多也是 O(n)。
因此比較困難的是,會切割幾次?!由於切割的大小會隨著 pivot 的不同,而產生不同的子數列,也使得切割次數不定。最佳的情況就是每次都剛好切割為相同大小的子數列,這時候就會使得切割次數為 log2n 次。假設每次切割都僅僅將原數列分為 0 與 n - 1(扣除 pivot),也就是說剛好 pivot 都取到該數列中的最大或最小值,則可能會有 n 次的遞回呼叫。所以 quick sort 的時間複雜度分為最佳時為 O(nlog2n),最差為 O(n2)。
既然 quick sort 最差會需要 O(n2) 的時間複雜度,那麼為何會被認為普遍是最快的排序演算法呢?再亂序的情況下,其實要出現剛好跑出 O(n2) 的可能性不高,但因為還是有這可能,所以我們都稱 quick sort 的平攤時間複雜度為 O(nlog2n),這是對於 quick sort 的排序時間所估算的期望值。
另外是空間複雜度,由於每次都會將數列分為兩個子數列,因此會申請兩個新的子數列記憶體空間,對於每個遞回來說空間複雜度是 O(n),根據前面的敘述可以知道遞回呼叫的次數最佳為 log2n 次,而最差為 n 次!因此空間複雜度也是最佳 O(nlog2n),最差為 O(n2)。
此外,其實可以透過實作的技巧來達到每次遞回時僅需要 O(1) 的空間複雜度,也就是所謂的 in-place 演算法。這時就僅需要看遞回呼叫的次數來決定空間複雜度,最佳 O(log2n),最差為 O(n)。
優化 Quick Sort
in-place version
首先先介紹優化空間複雜度的 in-place 版本,這個方法可以令我們不需要為子數列申請新的記憶體空間,使得每次遞回呼叫都僅需要 O(1) 的空間複雜度。另外 in-place 版本很神奇的地方是,它僅僅需要切割的操作,不必再有合併的操作了,因為在切割時就也做完合併了。in-place 版本的 quick sort 演算法:
- 從數列找出一個元素作為 pivot
- 將 pivot 移動到數列末端
- 設定一個指標指向數列前端,用來記錄小於 pivot 的元素的放置位置
- 接下來開始遍歷所有元素(除了 pivot)
- 若當前元素小於 pivot,就將該元素換到指標所指向的位置,且將指標往下一個位置移動
- 若當前元素大於等於 pivot 則跳過不做任何動作
- 當所有元素遍歷後,再將 pivot 與指標作指向的最後一個位置的元素交換
可以發現在 step 7 之前,原數列就已經被分為兩堆,前面那堆都是小於 pivot 的,而後面那堆都是大於等於 pivot 的。這時候進行 step 7 後,就會把 pivot 安插到兩堆中間,使得原數列呈現三個區塊 → [ 小於 pivot, pivot, 大於等於 pivot]。因此在遞回排序子數列後,將不必再進行合併的操作。
隨機化
前面的介紹可以發現,一旦 pivot 選的不好,很有可能造成 quick sort 出現 O(n2) 的時間複雜度。在一般的做法上,我們可能會每次都固定取數列中的某一個位置的值,例如:中間、最前面、最後面等等。這樣的話,quick sort 的基準就變成了資料本身的樣子,所以可以特別設計出讓 quick sort 跑特別慢的資料。所以當我們採用隨機化的策略來選擇 pivot 的話,那麼 quick sort 受到資料本身的影響也會較小,但仍有可能會出現 O(n2) 的情況。
Balanced Quick Sort
平衡快速排序法一樣是在改進 pivot 的選擇,採用的策略為取出數列最前端與最後端以及中間的元素,並以中間值作為 pivot。其好處為若是出現近似順序或近似是逆序的情況下,可以有效地將中間值找出來,使得切割次數可以維持在 log2 次。另外至少最明顯的優勢是,至少都可以將數列分為兩堆,最差就是分為兩堆為 1 與 n - 2(多扣除 pivot),不過這樣至少也能分兩堆,對效能上的增進也是不無小補!
Pseudo Code
Traditional Quick Sort
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// A is the sequence
function quick_sort( A ):
if length( A ) is empty
return
// choose pivot
pivot = A[ 0 ]
// divide
for i in [ 1, n )
if A[ i ] >= pivot
gt.append( A[ i ] )
else
lt.append( A[ i ] )
// sort sub-sequence
quick_sort( lt )
quick_sort( gt )
// merge
clear A to empty
A.append( lt )
A.append( pivot )
A.append( gt )
return
In-place Optimized
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// A is the sequence
// L is the close interval of left boundary
// R is the open interval of right boundary
function quick_sort( A, L, R ):
if ( L == R )
return
// choose pivot
pivot = A[ R - 1 ]
pos = L
// divde
for i in [L, R - 1)
if pivot >= A[ i ]
swap A[ i ] and A[ pos ]
pos = pos + 1
// orgazine order
swap A[ pos ] and A[ R - 1 ]
// sort sub-sequence
quick_sort( L, pos )
quick_sort( pos + 1, R )
return
Source Code
Traditional Quick Sort
Source code on gist.
In-place Optimized
Source code on gist.
效能比較
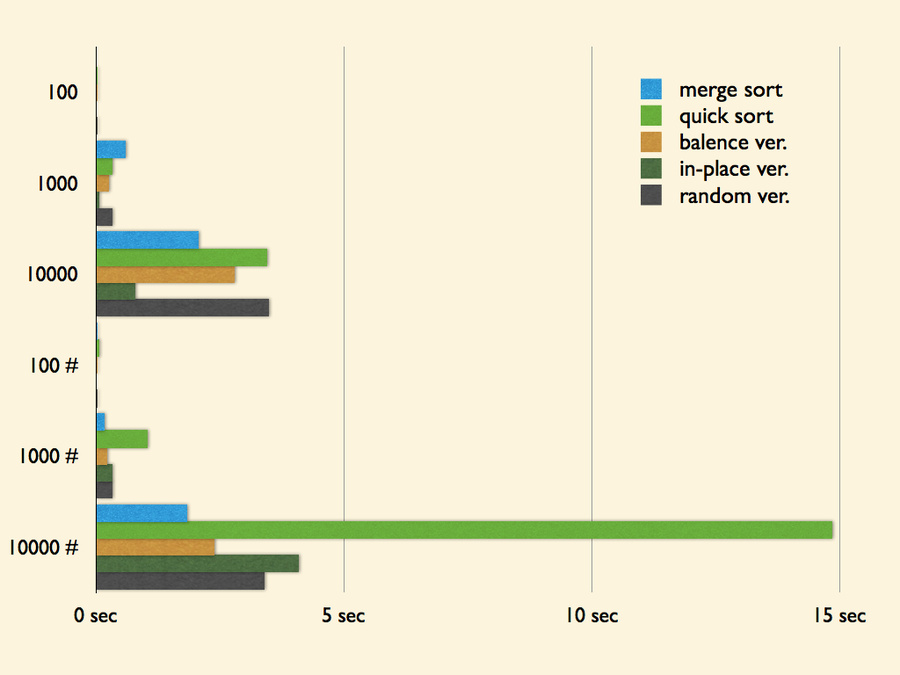
下面拿 merge sort 與不同種的 quick sort 進行效能比較!
| 資料數量 | merge sort | quick sort | balence ver. | in-place ver. | random ver. |
|---|---|---|---|---|---|
| 100 | 0.01 | 0.03 | 0.03 | 0.01 | 0.03 |
| 1000 | 0.60 | 0.33 | 0.26 | 0.07 | 0.33 |
| 10000 | 2.06 | 3.45 | 2.79 | 0.79 | 3.48 |
| 100 # | 0.02 | 0.06 | 0.02 | 0.01 | 0.03 |
| 1000 # | 0.17 | 1.03 | 0.23 | 0.33 | 0.32 |
| 10000 # | 1.84 | 14.85 | 2.39 | 4.09 | 3.40 |
以上測試資料皆為 100 組,單位為秒 (second)。# 標記的資料表示已接近排序好的數列。
與 merge sort 比起來,除了 in-place 版本的 quick sort 比較快外,其他都明顯略慢。我想根據時間複雜度來看,這似乎滿合理的,merge sort 本來就保證 O(nlog2n) 的時間,而 quick sort 則是平攤時間。至於 in-place 版本的效能較高,我想主因是省去了許多空間宣告與傳遞的負擔,所以也可以發現有資料量越大,效能增進越高的現象。
另外在近排序完成的數列中,quick sort 有點慘敗,尤其是選擇固定位置作為 pivot 的 quick sort。我想由於是幾乎排序好的數列,所以很容易選到趨近於極大或極小的數值,使得最後 quick sort 退化成了 O(n2) 的狀況。
在隨機選擇 pivot 的版本中就可以發現 quick sort 有恢復到亂序數列的水準,因此隨機選擇 pivot 的做法用來破壞原本資料的有序狀態效果不錯。另外可以看到 balance 版本的對於破壞有序的狀況效果更是不錯,因為他必定可以將數列分為兩個子數列,隨機選擇 pivot 其實還是有可能出現僅僅分割出一個子數列的狀況!
也可以發現在近排序完成的測試資料中,in-place 版本的效能似乎沒原本的高。由於該版本的 pivot 選擇也是固定的,所以應該會有像一般版本的 quick sort 一樣,有退化到 O(n2) 的情況,而在這樣的情況下,in-place 版本的效能高於一般版本許多了!
所以啊,要實作 quick sort 的最佳方法就是採用 balance 的方式選取 pivot,而且使用 in-place 的方式時做切割部分,應該就可以達到超高效率了吧!
以下的投影片中有 quick sort 的執行過程,有興趣可以前往參考!
Slide on Speaker Deck.
相關資料
Wikipedia 上的示意動畫: