中譯「合併排序法」,這次要介紹的可是個高效演算法,雖然在小量資料時可能不見得有明顯優勢,但資料量一大即可發現極大的差距!
Merge sort 採用 divide & conquer 的策略,該策略是不斷地將原數列剖半分為兩個較小的數列,並將兩個較小的數列排序好在進行合併。至於怎麼排序那兩個較小的數列呢?採用相同的策略,把數列在分為兩個較小的數列,並在排序好後進行合併!那麼,該剖半到什麼時候呢?其實切到數列只剩下一個元素在停止就好,因為當數列僅有一個元素時,就已經是個有序數列了,也就可回傳給上一個問題去進行合併!
於是,切割數列應該不成問題了,最大的問題就是合併了,這也是 merge sort 關鍵的地方,也是為什麼叫做 merge sort 的原因了!在取得兩個有序的數列後,進行合併的方式為同時枚舉兩數列內的元素,並進行比較後將較小的數值放入原數列中,持續該步驟直到枚舉過所有元素!具體的演算法流程,以下分為切割與合併兩個部分:
Divide
- 將數列對半切割
- 持續切割至數列僅剩一個元素
Conquer
- 當數列僅剩一個元素時即回傳
- 當數列不僅一個元素時,切割後待子數列排序完成
- 取得兩個有序子數列後,利用兩個指標指向該兩個子數列的起始元素
- 比較兩指標所指到的值,並將較小者放入原數列,並將指標指向下一個元素
- 若某一個指標已指到數列結尾,則按照順序將另一個子數列剩餘的元素放到原數列中
- 持續以上步驟即可排序完成
時間與空間複雜度
先來看時間複雜度,並從切割的部份開始,這部份根據實作會有所不同。如果從頭到尾都使用同一個陣列空間(例如:使用 global variable),且參數傳遞時僅傳送頭尾 index 值,那麼切割的時間複雜度僅為 O(1),直接將 index 相加除以 2 就可以得到切割位置的 index。若是每次切割都申請新的記憶體空間,則切割的時間複雜度為 O(n),因為需要遍歷所有元素且放入新的子數列中。至於合併的部分,合併是將兩個切割後的子數列進行合併,且枚舉比較兩子數列中的元素。因此每個元素都將被遍歷過,使得時間複雜度也為 O(n)。我們即可知道每一個遞迴式扣除排序子數列的時間的話,其時間複雜度為 O(n)。
那麼接下來要計算的是,遞迴式會執行幾次?詳細證明我不會,基本上就是計算 n 一直除以 2,除幾次會等於 1。反過來想 1 要乘以 2 幾次會等於 n,這應該很好理解,所以方程式就是 2x = n,求解 x 就可以得到 x = log2n。因此遞迴式最多也只會執行 log2n 次,配合上每次遞迴式所執行的時間,即可得到時間複雜度為 O(nlog2n)。
在空間複雜度上,一樣先從切割的部份開始,若每次遞迴式都使用相同的數列空間,那麼在切割時不需要額外申請空間,所以時間複雜度為 O(1)。若是每次都替子數列申請新的記憶體空間,那麼空間複雜度就為 O(n)。而在合併的部份,如果從頭到尾都使用相同的數列空間,但在合併時為了避免覆蓋還未比較的元素,勢必也需要另外申請一個長度為 n 的數列空間以存放合併結果,因此空間複雜度為 O(n)。若是有替子數列申請記憶體空間的話,在合併時就可以使用原來的數列空間,空間複雜度即為 O(1),因此每個遞迴式的空間複雜度皆為 O(n)。前面也算過了遞迴式會執行 log2 次,所以空間複雜度為 O(nlog2n)。
優化 merge sort
Natural Merge Sort
這邊介紹一個改進的方法,稱之為 natural merge sort。除了完全逆序的狀況外,該作法是利用數列內已存在的有序數列片段來減少切割的次數。若已知一個數列已有序,則該數列不需要再遞迴進行 merge sort 了,如此一來即可減少遞迴式的呼叫次數。而 natural merge sort 跟一般的 merge sort 的差異僅在切割的部份,合併部分皆相同。以下是其切割的演算法:
- 申請兩個新的數列空間,分別稱為 A 與 B,並設定數列 A 為使用中數列
- 依序遍歷數列元素,並將元素放入使用中數列
- 一旦當前遍歷的元小於上一個元素時,將使用中數列換為另一個數列,並將該元素放入
- 不斷的重複步驟 2 與步驟 3 直到所有元素被遍歷,並分配到子數列
- 若是切割後的子數列 A 與 B 中有任一個為空,表示原數列已有序,則不需在遞迴排序子數列
- 若子數列 A 與 B 皆不為空,則繼續遞迴排序
可以發現這樣的作法理論上可以省去許多的遞迴呼叫,除非完全逆序才有可能發生切割到一塊的狀況,否則幾乎都可以提前回傳不需要再進一步切割排序。
pseudo code
Tradition Merge Sort
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
function merge_sort( A ):
if length( A ) == 1
return
// divide
mid = length( A ) / 2
left = A[ i, mid )
right = A[ mid, length( A ) ]
merge_sort( left )
merge_sort( right )
// merge
for i in [ 0, n )
if left is empty
A[ i ] = first( right )
right = rest( right )
else if right is empty
A[ i ] = first( left )
left = rest( left )
else if first( left ) is less than first( right )
A[ i ] = first( left )
left = rest( left )
else
A[ i ] = first( right )
right = rest( right )
return
Natural Merge Sort
這邊我僅僅寫出切割的部分,合併的部分都僅用 merge 表示:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
function naturalMergeSort( A ):
B, C are empty sequence
CUR refer to B
LAST = A[ 0 ]
while A is not empty
if first( A ) >= LAST
append first(A) to CUR
LAST = first( A )
A = rest( A )
else
if CUR refer to B
CUR refer to C
else
CUR refer to B
LAST = first( A )
if B is empty or C is empty
return
naturalMergeSort( B )
naturalMergeSort( C )
A = merge( B, C )
Source Code
Tradition Merge Sort
Source code on gist.
Natural Merge Sort
Source code on gist.
效能比較
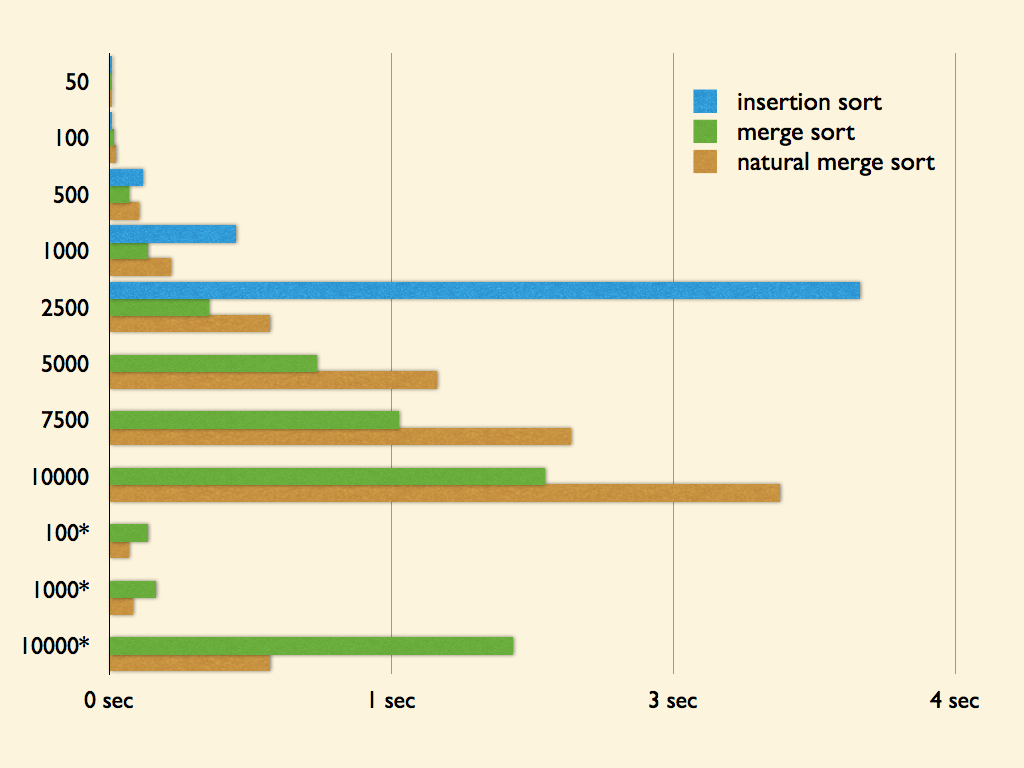
雖然拿時間複雜度 O(nlog2n) 跟 O(n2) 的比實在不公平,但還是拿 O(n2) 中最快的 insertion sort 來比較好了!
| 資料數量 | insertion sort | merge sort | natural merge sort |
|---|---|---|---|
| 50 | 0.01 | 0.01 | 0.01 |
| 100 | 0.01 | 0.02 | 0.03 |
| 500 | 0.16 | 0.09 | 0.14 |
| 1000 | 0.60 | 0.18 | 0.29 |
| 2500 | 3.55 | 0.47 | 0.76 |
| 5000 | x | 0.98 | 1.55 |
| 7500 | x | 1.37 | 2.18 |
| 10000 | x | 2.06 | 3.17 |
| 100 * | x | 0.18 | 0.09 |
| 1000 * | x | 0.22 | 0.11 |
| 10000 * | x | 1.91 | 0.76 |
以上測試資料皆為 100 組,單位為秒 (second),其中有星號的測試資料表示數列本身是由多組有序數列組成。欄位中標示 x 表示數值與其它欄位差異過大,為了避免圖表因該數據使得上現過大,而無法觀察細微部分,故移除該資料。
除了少於等於 100,發現有給 insertion sort 略勝的機會,但從 500 以後漸漸的可以發現 insertion sort 完全被虐爆。相信大家都可以感覺到 O(nlog2n) 與 O(n2) 得明顯差異了,並且隨著 n 的增長,效能的增進也更加明顯!
在表中可以發現 natural merge sort 似乎沒有預期的表現較佳,反而慘敗!!推估是在切割時耗費太多時間在進行比較,不像一般的 merge sort 直接對半切割,不需要進行任何比較操作。但在另一些特別設計為多組有序數列組成的測試資料中,即可發現 natural merge sort 還是有著顯著的效能增進!可惜大部份亂序資料的狀況下,要有多組有序數列組成的狀況可能就較少了。
以下的投影片中有 merge sort 的執行過程,有興趣可以前往參考!
Slide on Speaker Deck.
相關資料
Wikipedia 上的示意動畫:
