中譯「選擇排序法」,如同 bubble sort 與 insertion sort 一樣是非常直觀的排序法,而且我認為 selection sort 是最直覺最簡單的作法。這三個排序法都有著大量元素時,效率不佳的問題,畢竟其時間複雜度皆為 O(n2)。Selection sort 也是一個 in-place 演算法,運算時除了待排序的 n 個元素外,僅需要額外 O(1) 的空間!
Selection sort 與 insertion sort 很像,都是將數列分為已排序段與未排序段。不過與 insertion sort 不同的是,selection 並不是在已排序段中尋找插入位置,而是每次都在未排序段中尋找最小值,並放置在已排序段的末端。
演算法步驟:
- 設定已排序段為空
- 在未排序段中找出最小元素
- 將此最小元素放置於已排序段的末端
- 重複步驟 2 與步驟 3 直到未排序段為空
前面提過 selection sort 是一個 in-place 演算法,因此不需要額外的儲存空間。所以在實現上,我們可以將原數列的視為未排序段,而已排序段為空並且置於未排序段的前端。第一次找出最小值後,將該最小值與原數列的第一個交換,此時原數列的第一個元素為已排序段,而其他部分則為未排序段。第二次找出最小值後,將該最小值與原數列第二個元素交換(因為第一個元素為已排序段),此時已排序段則為原數列的第一個元素到第二個元素,依此類推。
時間與空間複雜度
根據演算法中可以發現要在未排序段中找 n 次最小值,這部份時間複雜度即為 O(n)。不過其實也可以說只要找 n - 1 次,因為最後一次未排序段也僅剩一個元素,該元素也必定是未排序段中最小值。接著在未排序段中尋找最小值時,未排序段最多會有 n 個元素,隨著每次迭代遞減,但仍舊是以 n 的數量級成長,因此在找尋最小值時也需要 O(n) 的時間,最終的時間複雜度即為 O(n2)。
根據演算法可以發現要枚舉 n - 1 個元素(除了第一個),所以沒舉元素需要 O(n) 的時間。而在尋找插入位置時,最多也需要 O(n) 的時間,不過這是在數列呈現完全逆序的狀況才有可能發生,所以最後時間複雜度即為 O(n2)。
空間複雜度上,計算上只需要額外的兩個暫存變數記錄最小值與交換位置,因此只增加 O(1) 的空間。所以其空間複雜度僅為 O(n)。
pseudo code
1
2
3
4
5
6
7
8
for i in [ 1, n )
minimum = A[ i ]
pos = i
for j in [ i + 1, n )
if minimum > A[ j ]
minimum = A[ j ]
pos = j
swap A[ i ] and A[ j ]
Source Code
Source code on gist.
效能比較
以下比較就拿 bubble sort 與 insertion sort 一起來比較吧!
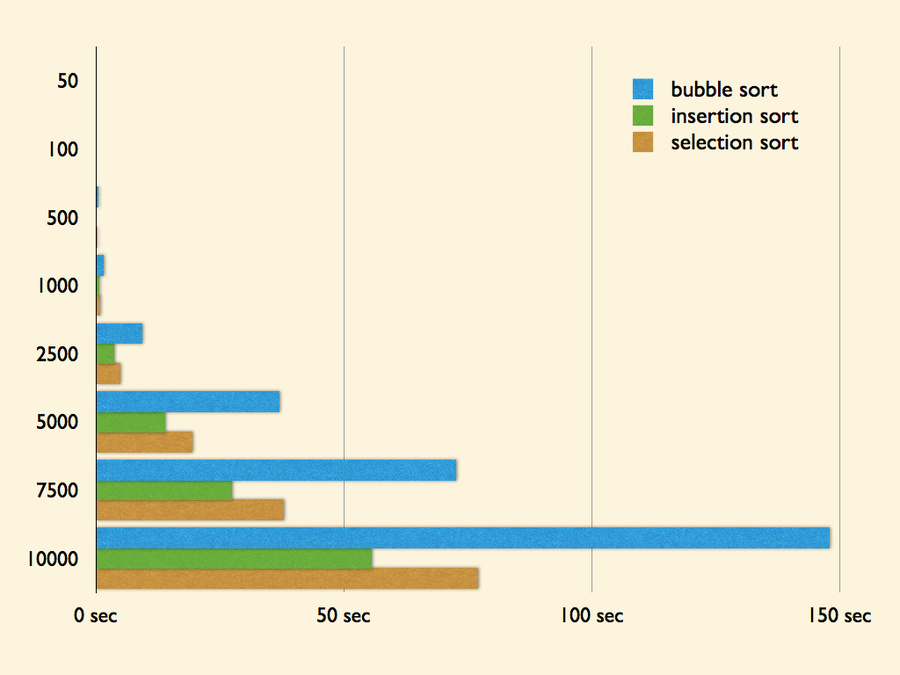
| 資料數量 | bubble sort | insertion sort | selection sort |
|---|---|---|---|
| 50 | 0.01 | 0.01 | 0.01 |
| 100 | 0.02 | 0.01 | 0.01 |
| 500 | 0.39 | 0.16 | 0.22 |
| 1000 | 1.51 | 0.60 | 0.82 |
| 2500 | 9.31 | 3.55 | 4.92 |
| 5000 | 37.05 | 14.00 | 19.40 |
| 7500 | 72.55 | 27.37 | 37.84 |
| 10000 | 147.95 | 55.61 | 77.07 |
以上測試資料皆為 100 組,單位為秒 (second)。
仔細分析可以發現 selection sort 會有 n(n - 1) / 2 次的比較與最多 n - 1 次最少 0 次的交換操作。如同 insertion sort 與 bubble sort 的差異一般,主要為運算量的差異,因此 selection sort 的效率也優於 bubble sort。至於 selection sort 略遜於 insertion sort 的原因,以交換操作與比較操作的次數來看,兩者擁有差不多的運算量,因此我認為 selection sort 會略遜於 insertion sort 的主要原因為需要額外紀錄最小元素的位置以用來交換。
以下的投影片中有 selection sort 的執行過程,有興趣可以前往參考!
Slide on Speaker Deck.
相關資料
Wikipedia 上的示意動畫:
