中譯「氣泡排序法」,相信這是大家第一個接觸的排序法,除了非常簡單之外,特色就是效率不佳,bubble sort 通常僅在少量元素時才擁有較高的效率。另外 bubble sort 是個 in-place 演算法,意思是該演算法不需要額外的空間做暫存。
演算法步驟:
- 從頭到尾依序枚舉相鄰數對
- 若該數對為一組逆序對,交換該數對內的元素
- 重複 n - 1 次後,數列排序完成
逆序對:若存在一數對 (p1, p2),且其中 p1 > p2,則稱該數對 (p1, p2) 為逆序對。
由於演算法是從數列前端向後端進行,每次碰到逆序對就進行交換。可以發現,經過第一次的迭代,最大的元素將會被移動到數列末端。而經過第二次迭代,次大的元素將被移動到最大元素前一個位置。而第三次迭代則會將第三大的元素移動到次大元素的前一個位置。依此類推,第 n 次迭代,會將第 n 大的元素移動到第 n - 1 大的元素前面。換句話說,第 n 次迭代會確定第 n 大的元素位置。
在這樣個情況下,演算法在每一次迭代都可以不需要在檢查那些已經確定位置的元素,也就是在末端的元素。並且經過每一次的迭代,就可以去掉一個要檢查的元素,也令每次迭代須檢查的數對數量遞減。此時,演算法的步驟將可改進為:
- 從頭到尾依序枚舉相鄰數對,並隨著迭代次數的增加,去除末端元素
- 若該數對為一組逆序對,交換該數對內的元素
- 重複 n - 1 次後,數列排序完成
時間與空間複雜度
根據演算法可以發現,枚舉數對需要 O(n) 的時間。而總共需要迭代 n - 1 次,因此也算作需要 O(n) 的時間,所以時間複雜度即為 O(n2)。
另外空間複雜度上,前面提過 bubble sort 是個 in-place algorithm,在計算上不需要花費其他額外的空間。因此其空間僅僅需要儲存原本數列的大小即可,其空間複雜度即為 O(n)。
優化 bubble sort
Bubble sort 在最差的情況下會需要執行 n2 次的交換操作,而這種情況只會發生在當整個數列呈現遞減的模樣。只有這樣的時候會有 n2 次的操作,但通常數列都是亂序的,出現完全遞減的情況較少,而且這種情況其實也不需要排序了。
既然數列是亂序的,那麼表示 bubble sort 其實是有可能在 n - 1 次之前就完成了排序!此時只要利用一個 flag 去記錄當前的迭代是否有執行交換操作,若沒有交換操作被執行,也表示該數列已排序完成,此時中止演算法將可以省去許多無謂的運算!
不過要在迭代 n - 1 次前就提前結束演算法的條件也是要在數列大部份是有序的,當然這機率其實也不高,所以這樣的改進其實不大。而在實際上的程式中,我發現效能反而變差,可能因為不僅沒有在 n - 1 次的迭代前完成排序,反而增加操作 flag 的時間。但也有可能,是我的程式碼寫太爛了!
pseudo code
一般版本
1
2
3
4
for i in [ 0, n - 1 )
for j in [ 0, n - 1 - i ]
if A[ j ] > A[ j + 1 ]
swap( A[ j ], A[ j + 1 ] )
flag 版本
1
2
3
4
5
6
7
8
for i in [ 0, n - 1 )
flag = false
for j in [ 0, n - 1 - i ]
if A[ j ] > A[ j + 1 ]
swap A[ j ] and A[ j + 1 ]
flag = true
if flag is false
break
Source Code
一般版本
Source code on gist.
flag 版本
Source code on gist.
效能比較
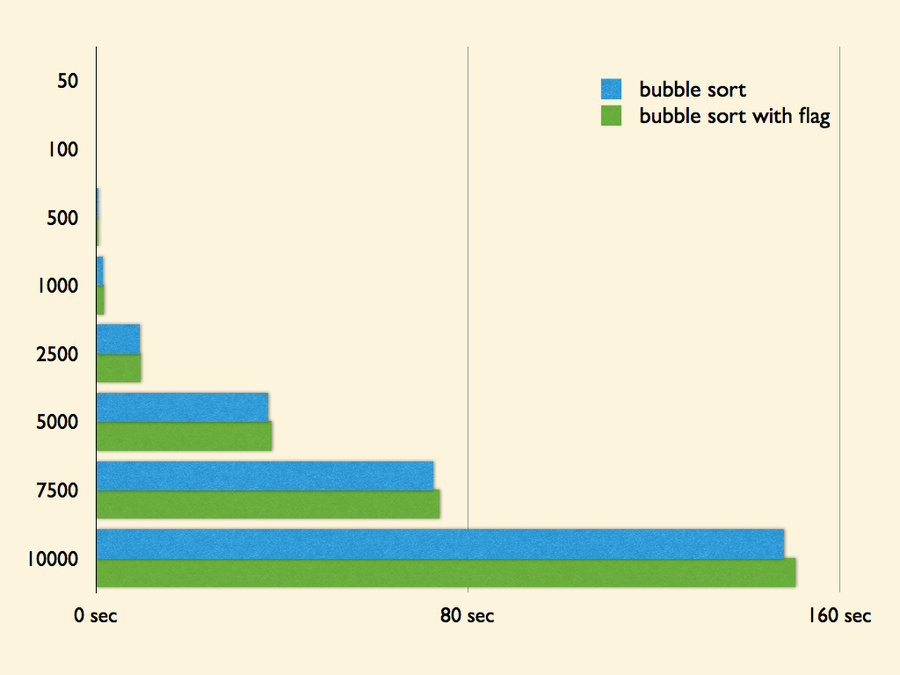
| 資料數量 | bubble sort | insertion sort |
|---|---|---|
| 50 | 0.01 | 0.01 |
| 100 | 0.02 | 0.02 |
| 500 | 0.39 | 0.40 |
| 1000 | 1.51 | 1.53 |
| 2500 | 9.31 | 9.46 |
| 5000 | 37.05 | 37.69 |
| 7500 | 72.55 | 73.79 |
| 10000 | 147.95 | 150.44 |
以上測試資料皆為 100 組,單位為秒 (second)。
在這邊可以發現使用了 flag 進行檢查不僅沒有提升效率,反而還輕微的降低了效率!可見在亂序數列情況下,要出現大部份有序的數列的機率不高,也因此要在 n - 1 次的迭代前結束演算法的可能性也不高!也因此使得 flag 的操作些微的拖累了效能!
以下的投影片中有 bubble sort 的執行過程,有興趣可以前往參考!
Slide on Speakerdeck.
相關資料
Wikipedia 上的示意動畫:
