中譯「插入排序法」,如同 bubble sort 一樣,也是非常直觀的排序演算法,但對於大量元素的情況下也表現不佳而少量元素有較佳的表現。與 bubble sort 一樣,都是 in-place 演算法,在運算時僅需要額外 O(1) 的空間。
Insertion sort 的概念為-將數列分為兩段,一段為已排序段,另一段則為未排序段。每次都從未排序段中取出一個元素,並在已排序段中找到適合插入的位置。
演算法步驟:
- 將第一個元素單獨做為已排序數列,其餘的元素為未排序段
- 枚舉未排序段的元素
- 從已排序段尾端向前端尋找到最後一個大於該枚舉元素的位置
- 最後將該枚舉元素插入該位置
當資料結構為陣列時,可能會納悶該怎麼插入比較有效率?一個很直覺得想法就是從枚舉元素的位置一步一步的向前一個元素交換,直到遇到小於等於該枚舉元素的值為止,但這麼一來將耗費許多交換的時間。仔細觀察可以發現,在 insertion sort 中每次進行交換時,其交換的兩個元素中,其中一個一定是該枚舉元素。
交換操作相信大家都很熟,假設有兩個元素 A 與 B 要進行交換,其交換過程如下:
- 利用一個變數 temp 暫存 A 的值
- 將 A 的值設為 B 的值
- 將 B 的值設為 temp 的值
如此一來就完成了一次交換,在上面的步驟中可以發現我們利用一個暫存變數來暫存 A 的值,接下來將 A 的值設為 B 的值。既然每次交換的數值中都會有該枚舉元素,那麼一來乾脆直接設一個暫存變數來儲存該枚舉元素,並在接下來的步驟中都直接執行第二部的賦值操作,並在找到插入的位置後,在執行第三部的賦值操作來將該枚舉元素插入正確的位置中。因此演算法如下:
- 將第一個元素單獨做為已排序數列,其餘的元素為未排序段
- 枚舉未排序段的元素,並利用一個暫存變數儲存該枚舉元素
- 從已排序段尾端開始將元素賦值給後一個位置,直到找到小於等於該枚舉元素的值時停止
- 最後將停止位置的值設為暫存值即完成插入
時間與空間複雜度
根據演算法可以發現要枚舉 n - 1 個元素(除了第一個),所以沒舉元素需要 O(n) 的時間。而在尋找插入位置時,最多也需要 O(n) 的時間,不過這是在數列呈現完全逆序的狀況才有可能發生,所以最後時間複雜度即為 O(n2)。
空間複雜度上,計算上只需要額外的一個暫存變數,因此只增加 O(1) 的空間。所以其空間複雜度僅為 O(n)。
優化 insertion sort
在尋找插入點這個步驟中,可以發現我們是在一個已排序數列中尋找。在有序數列中尋找枚舉元素的插入點,利用 binary search 的話,其實僅需要 O(log2n) 的時間!演算法最終可以達到 O(nlog2n) 的時間複雜度。
不過儘管可以利用 O(log2n) 的時間來找到插入位置,但在進行插入時,由於插入點之後的元素仍舊需要向後移動。因此還是會花費 O(n) 的時間,最後時間複雜度仍舊為 O(n2)。因此該優化大概僅是用於優化係數部分,當比較運算操作的負擔較賦值操作大石,多少可以進行些優化。真的要達到 O(nlog2n) 的時間複雜度的話,大概需要個較為特殊的資料結構,可以實現插入任意位置僅需要 O(1) 的時間,且要支援 random access,才可以進行 binary search。
pseudo code
1
2
3
4
5
6
7
for i in [ 1, n )
temp = A[ i ]
pos = i
while pos - 1 >= 0 && A[ pos - 1 ] > A[ pos ]
A[ pos ] = A[ pos - 1 ]
pos = pos - 1
A[ pos ] = temp
Source Code
Source code on gist.
效能比較
以下比較就拿 bubble sort 來比吧!
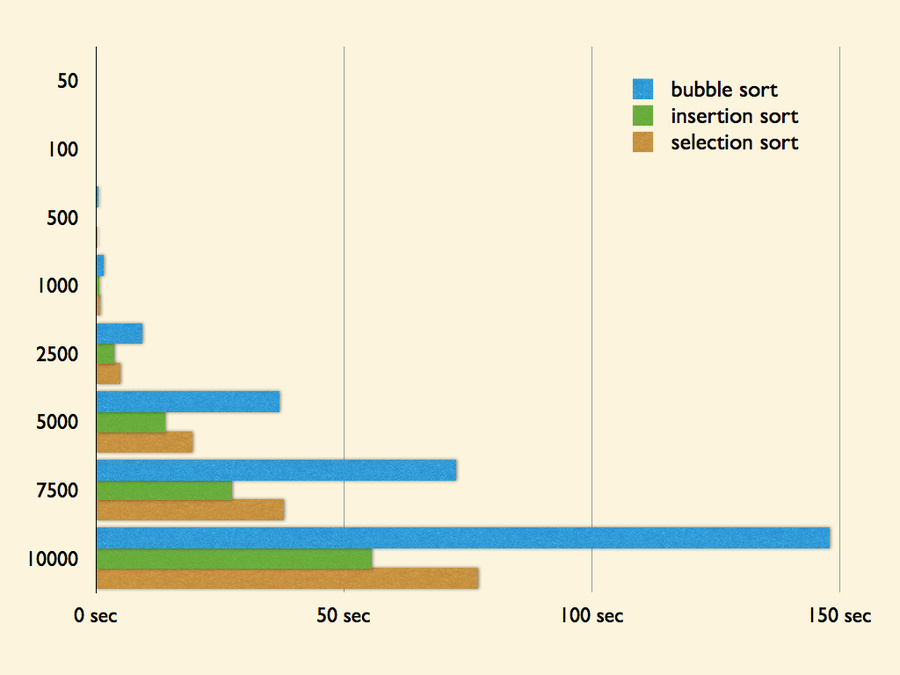
| 資料數量 | bubble sort | insertion sort |
|---|---|---|
| 50 | 0.01 | 0.01 |
| 100 | 0.02 | 0.01 |
| 500 | 0.39 | 0.16 |
| 1000 | 1.51 | 0.60 |
| 2500 | 9.31 | 3.55 |
| 5000 | 37.05 | 14.00 |
| 7500 | 72.55 | 27.37 |
| 10000 | 147.95 | 55.61 |
以上測試資料皆為 100 組,單位為秒 (second)。
與 bubble sort 相較起來效率提升許多,雖然兩者俱有相同的時間複雜度,但在實際上 bubble sort 的比較操作都將進行 n(n - 1) / 2 次。而 insertion sort 就算在最差的情況,數列完全是逆序的狀況下,頂多也只有 n(n - 1) / 2 次的比較操作。另外 bubble sort 的交換操作最差可能會進行 n(n - 1) / 2 次,而 insertion sort 沒有交換操作僅有賦值操作,賦值操作通常也較於交換操作快速,而且其賦值操作的次也僅有比較操作的次數加上 n - 1 次,這邊也計算了將數值存放於暫存變數與取出。可見雖然擁有相同的時間複雜度,但因運算量的差異導致了效能的差異,從表中可以發現效能約提升了 3 倍!
以下的投影片中有 insertion sort 的執行過程,有興趣可以前往參考!
Slide on Speaker Deck.
相關資料
Wikipedia 上的示意動畫:
