目前碩論使用了加速計，遇到一個問題是要求出當前加速計的姿態，也就是要知道現在加速計對於地面的傾角。

由於地球重力的影響，使得加速計無時無刻都受到重力的影響，並且將會根據姿態將其受力分到加速計中的 X 軸、Y 軸與 Z 軸。如下圖所示：

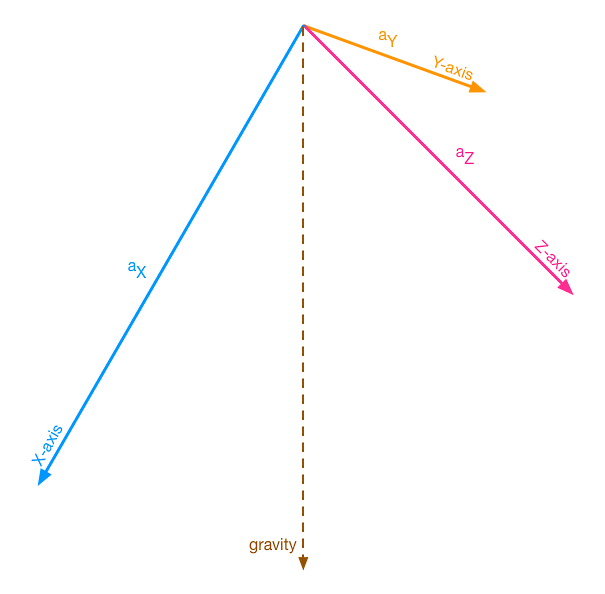
透過計算出當前姿態後，可以利用得到的傾角將加速計坐標系變換回現實坐標系。如下圖所示：

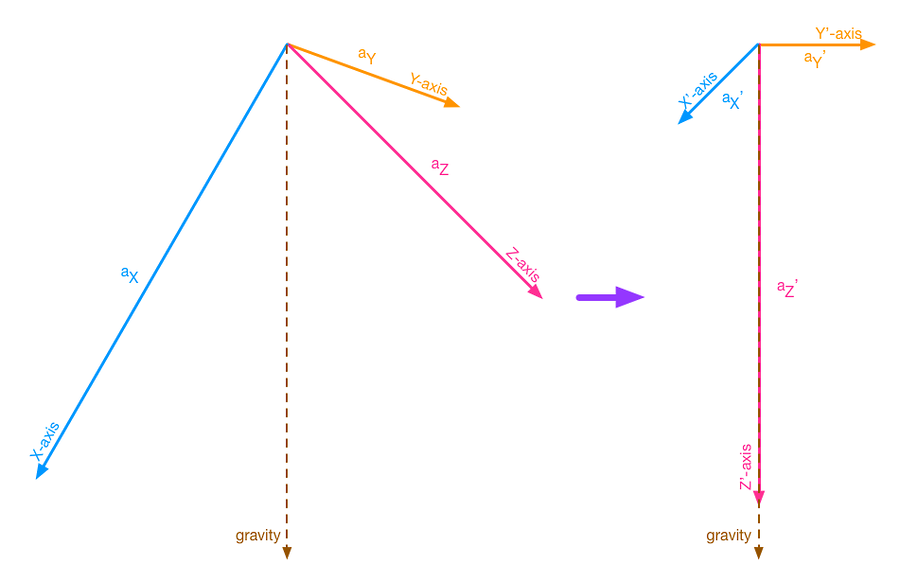
其中 Z’ 軸將與重力方向平行（與地表垂直），而 X’ 軸與 Y’ 軸將與地表平行（與重力方向垂直）。因此，a_Z’ 將等於 1 (g) 與重力相等，而 a_X’ 與 a_Y’ 將會等於 0。

要將加速度坐標系之 Z 軸對應到重力方向，需要進行兩次的旋轉，分別是對 X 軸旋轉以及對 Y 軸旋轉。所以接下來就是要求出用於對 X 軸旋轉之角度，以 roll angle 稱之並以 Φ 表示。以及對 Y 軸旋轉之角度，以 pitch angle 稱之並以 θ 表示。

Roll Angle (Φ)

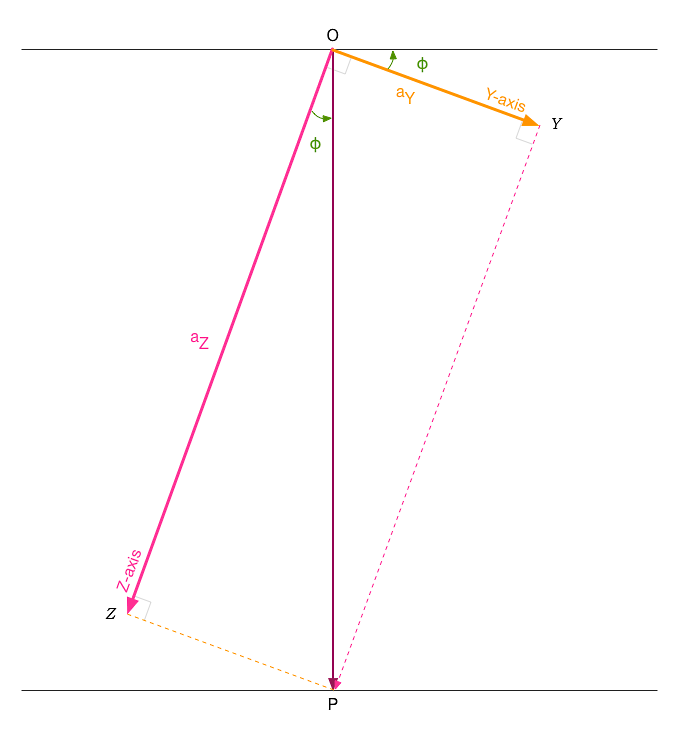
上圖為望向 YZ 平面之視圖，X 軸的正向即為眼睛往螢幕之方向。根據該圖，只要將整個坐標系沿著 X 軸逆時針旋轉 Φ 即可使得新 Y 軸（Y’ 軸）垂直於重力方向，令 Y 軸上的重力分量聚集到新 Z 軸（Z’ 軸）上。

至於 Φ 該如何求得？根據上圖，可以知道 ▱OYPZ 為一個矩形，因此 ZP 線段等於 OY 線段。可以算出 ∠ZOP 等於 tan^-1(a_Y/a_Z)，也就是 Φ。

$$\phi = tan^{-1}\dfrac{a_Y}{a_Z}$$

旋轉後，新的 Z 軸（Z’ 軸）上的分量將會是 √(a_Y² + a_Z²)。

$$a_Z' = \sqrt{a_Y^2+a_Z^2}$$

Pitch Angle (θ)

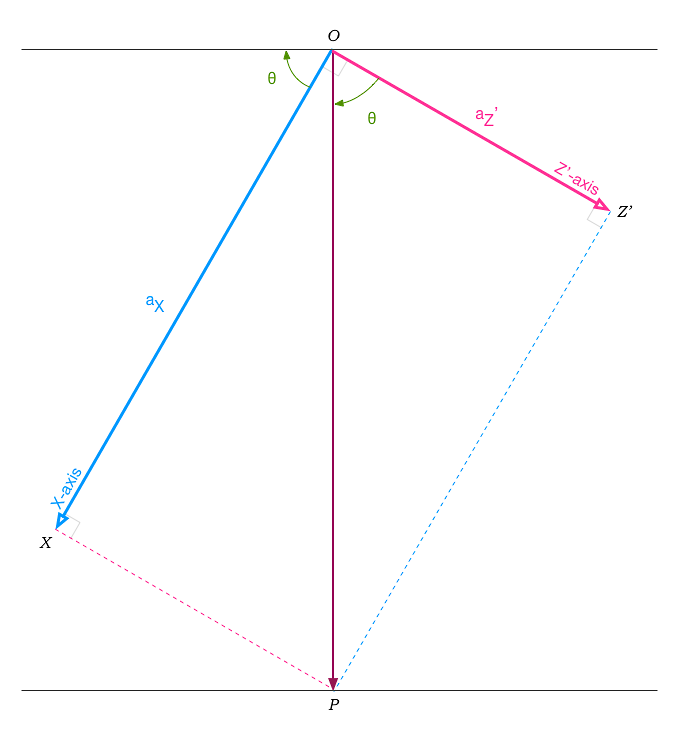
上圖為望向 XZ’ 平面之視圖，Y 軸的正向即為眼睛往螢幕之方向。同樣的只要將該坐標系沿著第一次旋轉後的新 Y 軸（Y’ 軸）順時針旋轉 θ 即可使得新 X 軸（X’ 軸）垂直於重力方向，令 X 軸上的重力分量積聚到新² Z 軸（Z’’ 軸）。

求 θ 的方法同求 Φ 的方法，知道 ▱OZ’PX 為一個矩形，因此 PZ’ 線段等於 OX 線段。可以算出 ∠Z’OP 等於 tan^-1(a_X/a_Z’)，也就是 θ。此外根據第一次旋轉的結果，可以得知 a_Z’ 等於 √(a_Y² + a_Z²)，直接帶入計算即可。

$$\theta = tan^{-1}\dfrac{a_X}{a_Z'} = tan^{-1}\dfrac{a_X}{\sqrt{a_Y^2+a_Z^2}}$$

旋轉過後的新² Z 軸（Z’’ 軸）則剛好與重力方向重疊，因此其受力將會等於 1 (g)。

經過以上的計算，我們就可以得到加速計的姿態，並利用求得的角度將加速計坐標重新對應到現實坐標系上。